РОЗГОРТКА КУБА
Означення.
Розгорткою куба називається шестиклітинкова плоска фігурка, в результаті згинання якої по
лініях клітинок можна отримати всю поверхню куба.
Варіанти розгорток куба.
Основна властивість розгортки куба.
Будь-яка розгортка куба може бути накреслена на
клітинковому папері мінімальним розміром прямокутника 3х4, якщо одна клітинка
дорівнює площі грані куба.
Якщо розгортку куба не можна перевертати на іншу
сторону,
то
кількість різних розгорток куба дорівнює 19.
2
|
1
|
3
|
3
|
4
|
4
|
4
|
5
|
5
|
|||||||||||
2
|
2
|
2
|
1
|
1
|
3
|
3
|
4
|
5
|
5
|
||||||||||
2
|
1
|
1
|
3
|
4
|
5
|
||||||||||||||
2
|
1
|
3
|
4
|
5
|
|||||||||||||||
6
|
7
|
7
|
8
|
9
|
9
|
10
|
10
|
||||||||||||
6
|
6
|
7
|
8
|
8
|
9
|
10
|
|||||||||||||
6
|
6
|
7
|
8
|
8
|
9
|
9
|
10
|
||||||||||||
6
|
7
|
7
|
8
|
9
|
10
|
10
|
|||||||||||||
11
|
12
|
13
|
14
|
15
|
|||||||||||||||
11
|
11
|
12
|
12
|
12
|
13
|
13
|
13
|
14
|
14
|
15
|
15
|
||||||||
11
|
12
|
13
|
14
|
14
|
15
|
15
|
|||||||||||||
11
|
11
|
12
|
13
|
14
|
15
|
||||||||||||||
16
|
16
|
17
|
18
|
19
|
|||||||||||||||
16
|
16
|
17
|
18
|
18
|
19
|
||||||||||||||
16
|
16
|
17
|
17
|
18
|
18
|
19
|
19
|
||||||||||||
17
|
18
|
19
|
|||||||||||||||||
17
|
19
|
Якщо розгортку можна перевертати на іншу сторону,
то кількість різних розгорток куба дорівнює 11.
2
|
1
|
3
|
3
|
4
|
4
|
4
|
11
|
||||||||||||
2
|
2
|
2
|
1
|
1
|
3
|
3
|
4
|
11
|
11
|
||||||||||
2
|
1
|
3
|
4
|
11
|
|||||||||||||||
2
|
1
|
1
|
3
|
4
|
11
|
11
|
|||||||||||||
6
|
7
|
7
|
14
|
12
|
|||||||||||||||
6
|
6
|
7
|
14
|
14
|
12
|
12
|
12
|
||||||||||||
6
|
6
|
7
|
14
|
14
|
12
|
||||||||||||||
6
|
7
|
7
|
14
|
12
|
|||||||||||||||
16
|
16
|
17
|
|||||||||||||||||
16
|
16
|
17
|
|||||||||||||||||
16
|
16
|
17
|
17
|
||||||||||||||||
17
|
|||||||||||||||||||
17
|
Самостійна робота учнів за варіантами
Кожній парі учнів пропонується задача з геометрії, для розв’язання якої необхідно побудувати малюнок, користуючись графічним редактором Paint.
(Малюнок многогранника з’являється на екрані монітора разом з умовою задачі ). Учень будує переріз многогранника площиною, використовуючи інструменти у заданому редакторі.
I варіант
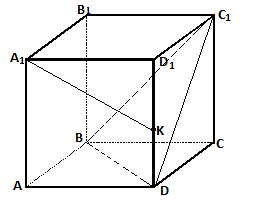 | За допомогою малюнка відповісти на питання.Дано: куб ABDCA1B1C1D11) Чи перетинає пряма A1B1 пряму AD; площину ВС1D?2) Де знаходиться точка перетину прямої A1K з площиною ABC?3) Чи перетинаються пл |
На ребрах АА1 і СС1 паралелепіпеда АВСDA1B1C1D1 дано точки K і P, такі що AK = KA1, CP:PC1 = 1:2. Побудуйте переріз паралелепіпеда площиною D1KP.
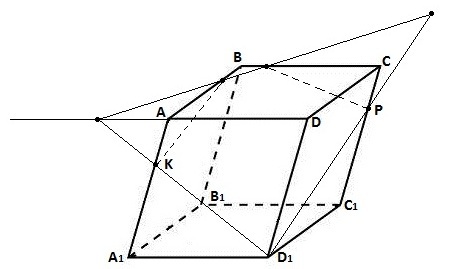
II варіант
Точка Х ділить ребро АВ куба АВСDA1B1C1D1 у відношенні 2:3 = AX:XB. Побудуйте переріз куба площиною, яка паралельна площині AA1C1 і проходить через точку X.
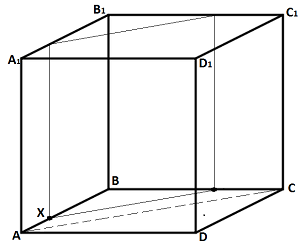
IІI варіант
 | За допомогою малюнка відповісти на питання.Дано: куб ABDCA1B1C1D11) Чи перетинає пряма A1B1 пряму AD; площину ВС1D?2) Де знаходиться точка перетину прямої A1K з площиною ABC?3) Чи перетинаються пл |
Побудуйте переріз куба АВСDA1B1C1D1 площинами, які проходять через вершини A, D1, C та A1,B,C1. Доведіть, що перерізи паралельні.
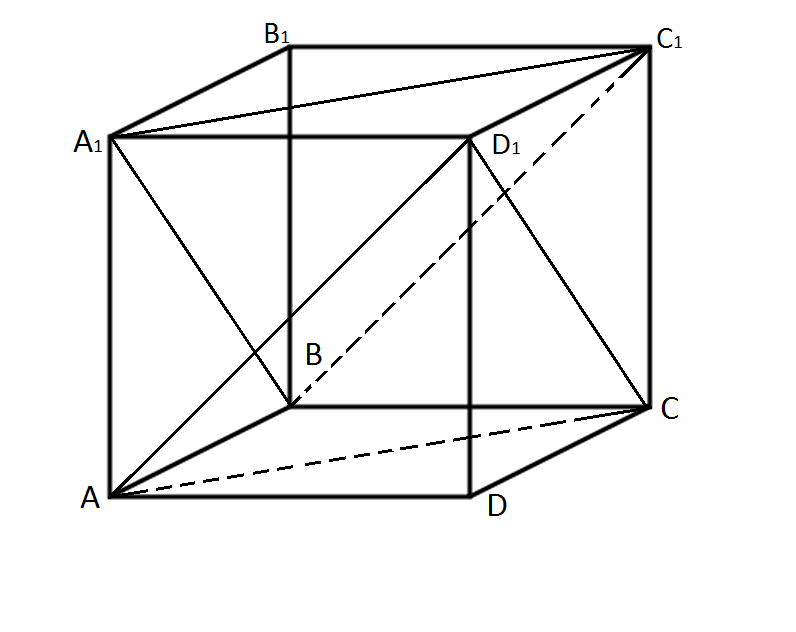
6. Домашнє завдання (з’являється на екрані монітору )
1. АВСDA1B1C1D1 – прямокутний паралелепіпед, AB = CD = a, K – середина ребра A1B1 і ∠KAC = α.
Побудуйте переріз паралелепіпеда площиною, яка проходить через точки A1C1K і знайдіть його площу. Обчисліть,якщо а = 13дм, α = 75⁰.
2. Записати алгоритм виконання малюнка з самостійної роботи.
Немає коментарів:
Дописати коментар