пряма Ейлера у трикутнику

З історії функцій

З історії функцій

     Поняття функції виникло в математиці порівняно недавно. Для того щоб прийти до розуміння доцільності його введення й одержати перші досить чіткі означення, потрібні були зусилля відомих математиків декількох поколінь. Революційні зміни в математиці, що відбулися в ХVІІ сторіччі, викликані роботами багатьох вчених, що представляють різні країни і народи. Але в першу чергу варто назвати імена :

П. Ферма (1601—1665),


Р. Декарта (1596—1650),


И. Ньютона (1643—1727),


Г. В. Лейбніца (1646—1716).

     Необхідні передумови до виникнення поняття функції були створені в 30-х роках ХVII в., коли виникла аналітична геометрія, що характеризується, на відміну від класичних методів геометрів Древньої Греції, активним залученням алгебри до рішення геометричних задач. Практично одночасно (і незалежно один від одного) французькі математики П. Ферма і Р. Декарт помітили, що введення системи координат на площини і завдання фігур їхніми рівняннями дозволяють звести багато задач геометрії до дослідження рівнянь геометричних фігур. На честь Декарта, що дав розгорнутий виклад нового методу в книгах «Геометрія» і «Міркування про метод», прямокутна система координат пізніше була названа декартовою. Істотно помітити, що одночасно формувалася й алгебра, створювалося «буквене числення», те саме, за допомогою якого зараз перетворюються алгебраїчні вирази, розв”язуються рівняння, текстові задачі і т. п.
   Великий англійський учений, математик і фізик І. Ньютон, досліджуючи залежності координат точки, що рухається, від часу, фактично вже займався дослідженням функцій. Хоча не він увів це поняття, Ньютон ясно усвідомлював його значення. Так, у 1676 р. він відзначав: «Я не міг би, звичайно, одержати цих загальних результатів, перш ніж не відвернувся від розгляду фігур і не звів усе просто до дослідження ординат» (тобто фактично функцій від часу).

    Сам термін «функція» уперше зустрічається в рукописі великого німецького математика і філософа Г. Лейбніца — спочатку в рукописі (1673 р.), а потім і в друкованому вигляді (1692 р.). Латинське слово function переводиться як «здійснення», «виконання» (дієслово fungor переводиться також словом «виражати»). Лейбніц увів це поняття для назви різних параметрів, зв’язаних з положенням точки на площині. У ході переписування Лейбніц і його учень — швейцарський математик И. Бернуллі (1667—1748)поступово приходять до розуміння функції як аналітичного виразу й у 1718 р. дають таке означення: «Функцією змінної величини називається кількість, складена яким завгодно способом з цієї перемінної і постійних».

   Л. Эйлер у своїй книзі «Введення в аналіз» (1748 р.) формулював означення функції так: «Функція перемінної кількості є аналітичне вираження, складене яким-небудь способом з цієї перемінної кількості і чисел чи постійних кількостей».

Эйлер же ввів і прийняті зараз позначення для функцій.

Сучасне означення числової функції, у якому це поняття вже звільнялося від способу завдання, було дано незалежно один від одного російським математиком Н. И. Лобачевским (1834 р.)

Задачі на знаходження відстані між прямою та площиною

Відстань між прямою та площиною

1.     Діагоналі ромба дорівнюють 12 см і 16 см. Точка М, знаходиться поза площиною ромба і віддалена від усіх сторін ромба на 8 см. Знайдіть відстань від точки М до площини ромба.

2.     Площа рівнобедренного трикутника дорівнює 768 см², а його основа 48 см. Точка простору знаходиться на відстані 60 см від площини трикутника і рівновіддалена від усіх його вершин. Знайти відстань від цієї точки до вершин трикутника.

3.     У рівнобедренному трикутнику кут при вершині дорівнює 120°, а бічні сторони – 10 см. Поза трикутником дано точку, яка віддалена від усіх його вершин на 26 см. Знайдіть відстань від цієї точки до плошини трикутника.

4.      Із вершини прямого кута прямокутного трикутника проведено перпендикуляр до площини трикутника. Гіпотенуза трикутника дорівнює 12 см, а один із гострих кутів - 60°. Знайдіть відстань від верхнього кінця перпендикуляра до вершин гострих кутів трикутника, якщо довжина перпендикуляра дорівнює 8 см.

5.     Периметр правильного трикутника дорівнює 36Ö3, а відстані від д деякої точки до кожної із сторін трикутника 10 см. Знайдіть відстань від цієї точки до площини трикутника.

6.     Із точки до площини проведено дві похилі, кут між якими дорівнює 60°, а кут між їх проекціями – 90°. Довжини проекцій  похилих на площину дорівнюють – 3 см кожна . Знайдіть відстань від точки до площини .

7.     Із вершини гострого кута прямокутного трикутрника АВС(  ÐС=90°) проведено перпендикуляр АD до його площини. Знайдіть відстані від точки D до вершин В і С, якщо АС = 15 см , ВС = 8 см , АD = 12 см.

8.     Із точки , віддаленої від площини на 12 см, проведено до неї дві похилі довжиною 13 і 12Ö2 см. Кут між проекціями цих похилих на площину дорівнює 90°. Знайдіть відстань між основами похилих .

9.     Більша сторона рівнобічної трапеції дорівнює 50 см, а її діагоналі перпендикулярні до бічних сторін. Точка віддалена від площини трапеції на відстань 60 см і рівновіддалена від її вершин . Знайдіть відстані від цієї точки до вершин трапеції .

10.                       Із точки до площини проведено дві похилі . Довжина першої похилої дорівнює 13 см, а довжина її проекції – 5 см. Кут між проекціями дорівнює 120 , а довжина відрізка , що сполучає основи похилих, - 19 см. Знайдіть довжину другої похилої.

11.                        Відрізок довжиною 25 см операється кінцями на дві взаємно перпендикулярні площини. Відстані від кінців відрізка до площини дорівнюють 15 см і 16 см. Знайдіть проекції відрізка на кожну із площин.

12.                       Із точки до площини проведено дві похилі, довжинин яких 10 см і 17 см. Різниця прекцій цих похилих дорівнює 9 см. Знайдіть довжини проекцій даних похилих.

13.                       Із точки простору до площини проведено дві похилі, довжини яких віносяться, як 5:6. Знайдіть відстань від точки до площини , якщо відповідні проекції похилих дорівнюють 4 см і 3Ö3 см.

14.                       Дано трикутник зі сторонами 26 см , 28 см і 30 см . Точка М віддалена від усіх сторін трикутника на 17 см і проектується у внутрішню точку трикутника. Знайти відстань від точки М до площини трикутника. 

15.                       Площа ромба дорівнює 120 см²,  а його сторона – 12 см. Точка простору рівновіддалена від сторін цього ромба на 13 см. Знайти відстань від цієї точки до площини ромба.

16.                       Із точки  до площини проведено дві похилі , які дорівнююють 3Ö2 см кожна. Кут між похилими дорівнює 60⁰ , а кут між їх проекціями – прямий . Знайти відстань від цієї точки до площини.

17.                       Трапеція вписана в коло, причому менша її основа , що дорівнює 16 см, стягує дугу в 60⁰. На відстані 12 см від площини трапеції знаходиться точка, рівновіддалена від усіх вершин трапеції. Знайти відстань від цієї точки до вершин трапеції.

18.                       До площини прямокутника АВСД через його вершину Д  проведено перпендикуляр ДК, кінець якого К віддалений від сторони АВ на 2,4 см, від сторони ВС – на 2,8 см., від вершини В – на 3,6 см. Знайдіть ДК.

19.                       Основа і висота рівнобедреного трикутника дорівнює 4 см. Дана точка знаходиться на відстані 6 см від площини трикутника і на однаковій відстані від його вершин. Знайдіть цю відстань.

20.                       Із точки  до площини прямокутника зі сторонами 6 см і 8 см, проведено перпендикуляр довжиною 24 см. Основа перпендикуляра – вершина одного з кутів прямокутника. Знайти відстань від даної точки до протилежної вершини прямокутника.

21.                       Кінці відрізка лежать на двох взаємно перпендикулярних площинах. Проекції відрізка на кожну із площин відповідно дорівнюють Ö369 см і 20 см. Відстань між основами перпендикулярів, проведених із кінців відрізка до площин, дорівнює 12 см. Знайдіть довжину даного відрізка.

22.                       Сторони трикутника дорівнює 36 см, 25 см і 29 см. Відстань від деякої точки до площини трикутника дорівнює 15 см. Відстань від цієї точки до сторін трикутника рівні. Знайти ці відстані.

23.                       Висота рівностороннього трикутника дорівнює 9 см. Точка знаходиться на відстані 8 см від площини трикутника і рівновіддалена від його вершин. Знайдіть відстані від цієї точки до вершин трикутника.

24.                       З точки, що знаходиться на відстані 4 см від площини, проведено до цієї площини дві похилі довжиною 5 см і 4Ö5 см. Кут між проекціями цих похилих дорівнює 60⁰. Знайти відстань між основами похилих.

25.                       Стоорони трикутника дорівнює 13 см, 14 см і 15 см. Точка простору віддалена від кожної сторони цьго трикутника на 5 см. Знайдіть відстань від цієї точки до площини трикутника.

26.                       Основи рівнобічної трапеції дорівнюють 14 см і 50 см, а бічна сторона – 30 см. Знайдіть відстань від площини трапеції до точки, віддаленої від кожної вершин на 65 см.

27.                       У трикутнику АВС сторона АВ = 15 см, АС = 13 см, СВ = 14 см. З вершини А проведено до його площини перпендикуляр, довжина якого дорівнює 16 см. Знайти відстані від кінців перпендикуляра до сторони ВС.

ВЗАЄМНЕ РОЗМІЩЕННЯ ДВОХ ПЛОЩИН.

ВЗАЄМНЕ   РОЗМІЩЕННЯ  ДВОХ   ПЛОЩИН.

ОЗНАКА   ПАРАЛЕЛЬНОСТІ   ПЛОЩИН

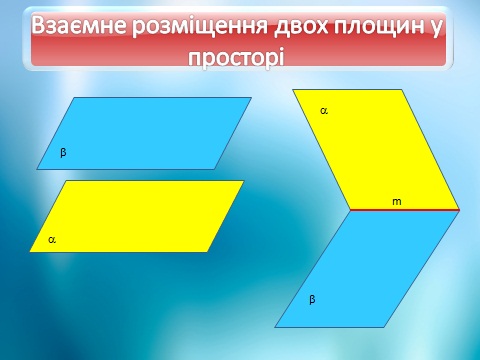
Існує три випадки взаємного розміщення двох площин у просторі. Дві площини:

1) збігаються, якщо вони мають три спільні точки, які не належать прямій;

2) перетинаються, якщо вони різні і мають спільну точку;

3) дві площини не мають спільної точки.

Доведемо, що можливий третій випадок взаємного розміщення двох площин: дві площини не мають спільної точки.

У площині α проведемо дві прямі а і b (мал. 30), які перети­наються. Через точку В₁, яка не належить α, проведемо прямі а₁||а і b₁||b;  через а₁ і b₁  проведемо площину b.

Доведемо (від супротивного), що α i β не мають спільної точки. Припустимо, що М - спільна точка площин α i β. З аксіоми  випливає, що їх перерізом є деяка пряма с. Але площина α прохо­дить через а, площина β - через а₁, причому а||а₁. Тоді с||а. Таким самим способом доводимо, що с||b. Ми прийшли до суперечності з аксіомою паралельних: у площині  α через точку В проходять дві прямі а і b, які перетинаються і паралельні прямій с. Отже, площини α i β не мають жодної спільної точки. ■

Таким чином, для двох площин α i β можливі лише три випадки:

1) α = β; 2) α Çβ = а; 3) α Çβ =Æ.

Перший і третій випадки ми знову об'єднаємо.

Означення. Дві площини називаються паралельними, якщо вони не мають спільної точки або збігаються.

Позначення паралельності площин α i β: а||β.
Теорема (ознака паралельності  двох площин).  Якщо   дві прямі,   що   перетинаються,   однієї   площини   відпо­відно паралельні двом прямим іншої площини, то ці площини паралельні.        

Істинність ознаки для випадку, коли дані площини різні, ви­пливає з наведеного вище міркування. Запишемо символічно це доведення (мал. 30).

Дано: аÎα,  bÎα, аÇb = В;  а₁Îβ, b₁Îβ; а₁||а;  b₁||b.

Довести: α||β.

Доведення   (від супротивного).   Нехай α Çβ = c.  Маємо:

 (а||а₁ аÎα, а₁ Îβ) тоді с||а; (теорема 4). (b||b₁ bÎα, b₁Îβ) тоді с||b.

Ми прийшли до суперечності з аксіомою паралельних прямих.
Отже, α||β.  .

Площини α і β можуть  збігатися (мал. 31). і в цьому випадку ознака справджується: адже збіг площин є окремий випадок їх паралельності. ■

Задачі з теми ПАРАЛЕЛЬНІСТЬ ПЛОЩИН

1. Яким може бути взаємне розміщення площин α i β, коли відомо, що:

1) деяка пряма b, що лежить у площині α, не лежить у площині β; (дві площини перетинаються або паралельні, якщо ці площини не співпадають).

2) жодна з прямих, що лежать у площині α, не лежить у площині β? (паралельні, якщо ці площини не співпадають).

2. Чи правильне твердження, що площини паралельні, якщо:

1) пряма, яка лежить в одній площині, паралельна прямій другої площини; (ні)

2) дві прямі, які лежать в одній площині, відповідно паралельні двом прямим іншої площини(ні)?

3. Покажіть моделі паралельних площин на предметах класної обстановки.

4. Доведіть паралельність площин, в яких розміщені проти­лежні грані паралелепіпеда.

5. Діагональ і сторона многокутника паралельні площині α. Чи правильне твердження, що площина многокутника паралельна площині α, якщо многокутник має:

1) чотири сторони; (так)

2) п'ять сторін; (ні)

3) n сторін (n > 5) (ні)?

6. Дано тетраедр АВСD; точки М, N, Р є серединами ребер DА, DВ, DС. Доведіть, що пл.(МNР)||пл.(АВС).

7. Прямі а, b, с, які не лежать в одній площині, мають спільну точку О. На кожній з цих прямих узято з різних боків від точки О відповідно пари точок: А₁ і A₂, В₁ і В₂, С₁ і С₂. Доведіть, що пло­щини А₁В₁С₁ і А₂В₂С₂ паралельні, якщо OА₁=OА₂, OВ₁ = OВ₂, ОС₁ =OС₂.

8. 1) Доведіть, що коли кожна з двох прямих, які перетина­ються і лежать в площині α паралельна площині β, то ці площини паралельні.

2) Горизонтальність встановлення лімба кутомірних інстру­ментів перевіряють, користуючись двома рівнями, розміщеними на одній площині (мал. 32). Чому рівні розміщують на діаметрах?

ТЕОРЕМИ   ПРО   ПАРАЛЕЛЬНІ   ПЛОЩИНИ

Теорема. Якщо дві паралельні площини перетнуто третьою площиною, то лінії перетину паралельні.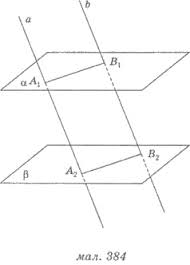

Дано:   α||β ,    αÇγ = c,   β Çγ = b. Довести:   c||b.

Теорему доведіть самостійно (мал. 33). Досить розглянути ви­падок, коли площини α i β різні.

Теорема. Через дану точку можна провести одну і тільки одну площину, паралельну даній площині.

Доведення. Нехай точка А не належить а (мал. 34). Існування площини β, що проходить через точку А і паралельна площині α, вже було доведено. Доведемо єдиність такої площини.

Припустимо, що через точку А проходить площина β₁, яка паралельна α і не збіга­ється з β. Тоді за аксіомою  площини β і β₁, перетинаються по деякій прямій m (мал- 34). Проведемо в площині α пряму l, мимобіжну з m через l і А проведемо площину γ. Ця площина перетне площини β і β₁ відповідно по прямих b і b₁. Згідно з попередньою теоремою  маємо: b||l і b₁||l, що суперечить аксіомі паралельних прямих. Отже, припущення про існування площи­ни β₁ неправильне.

Істинність теореми для випадку, коли точка В належить площині α, не потребує докладних пояснень. У цьому випадку єдиною площиною, яка проходить через В і паралельна α, є та сама площина α.

Наслідок. Якщо кожна з двох за­даних площин паралельна третій площині, то дані дві площини паралельні між собою.

Доведіть самостійно, наприклад, спо­собом  від супротивного 

Задача. Через кожну з двох мимобіжних прямих провести площину так, щоб ці площини були паралельні.

Розв'язання. Через довільну точ­ку М прямої а проведемо пряму а₁ пара­лельну прямій b (мал. 36); через прямі а і а₁ проведемо площину α. Аналогічно проводимо площину β.   Площини α і β паралельні згідно з ознакою паралельності площин.

Задача має єдиний розв'язок (цього не будемо доводити).

Задачі

1. Яким може бути взаємне розміщення прямих а і b, кожна  з яких лежить в одній з двох різних паралельних площин?(або мимобіжні або паралельні)

2. Чи можуть бути паралельними прямі, утворені внаслідок перетину двох площин, які перетинаються, третьою площиною? (так)

3. Доведіть, що коли площина перетинає одну з паралельних пло­щин, то вона перетинає і другу.

4. Доведіть, що коли пряма пере­тинає одну з двох паралельних пло­щин, то вона перетинає й другу.

5. 1) Закінчіть формулювання теореми: «Два паралельні відрізки,
кінці яких належать різним паралель­ним площинам, мають...»(однакові довжини). Доведіть цю теорему.

2) Чи можуть мати однакові дов­жини два непаралельні відрізки, кін­ці яких належать різним паралель­ним площинам? (так).

6. Через дану пряму проведіть площину, паралельну даній площині. Дослідіть розв'язок.

Дано:  α||α₁,  β||β₁  βÇα = c. β₁Çα₁= c₁. 

Довести:   c||c₁  .

7. Побудуйте переріз паралеле­піпеда АВСDА₁В₁С₁D₁ площиною α,

що проходить через вершини А, С і точку М ребра A₁В₁ 

Розв'язання. Переріз площини α з двома гранями діста­немо, провівши відрізки АС і АМ. Лінія перетину площини а з гранню А₁В₁С₁D₁ паралельна (АС), тому про­водимо МN||АС. Нарешті, будуємо відрізок NС. Трапеція АМNС - шуканий переріз. Якщо М — В₁, то шуканий переріз є трикутник АВ₁С, а якщо М = А₁, то переріз — паралелограм АА₁С₁С. Розв'язок єдиний.

8. Побудуйте переріз тетраедра АВСD площиною, що прохо­дить через внутрішню точку М ребра АВ  і  паралельна грані AВС.

9. Через вершину тетраедра проведено площину, паралельну протилежній грані. Побудуйте лінії перетину цієї площини з пло­щинами решти граней тетраедра.

10. На ребрах АD і В₁С₁ паралелепіпеда АВСDА₁В₁С₁D₁  дано внутрішні точки М і N. Побудуйте переріз паралелепіпеда пло­щиною, що проходить через точки М, N і паралельна ребру АВ.

11. Побудуйте   переріз   куба   АВСDА₁В₁С₁D₁  площиною,   яка

проходить  через  вершину В і середини ребер СС₁ і А₁D₁.

 

ПАРАЛЕЛЬНА ПРОЕКЦІЯ ФІГУРИ.

ВЛАСТИВОСТІ ПАРАЛЕЛЬНОЇ  ПРОЕКЦІЇ

У цьому і наступному параграфах сформульовано правила зо­бражень, якими користуються в стереометрії. Насамперед введемо кілька нових понять.

Нехай дано площину a і  пряма l яка   перетинає a   Візьмемо довільну точку А₁, через і. проведемо пряму l₁, паралельну прямій l.   Пряма   l₁,   перетне  a в деякій точці А. Утворену таким способом точку  А назвемо проекцією точки А₁ на площину a при проектуванні паралельно прямої l (коротше, точка   А - паралельна  проекція точки А₁).

Означення. Пара­лельною проекцією фігури Ф₁ назвемо    множину   Ф    паралельних проекцій усіх точок цієї фігури.

 Уявлення про паралельну проекцію   фігури   матимемо,   розгля­даючи тінь, яку кидає   на  стіну в звичний день картонна або дротяна  модель цієї фігури 

Сонячні промені можна наближено вважати паралельними через велику відстань від Сонця до Землі.
Модель   правильного шестикутника    А₁В₁С₁D₁E₁F₁    кидає на стіну тінь  у вигляді многокутника    АВСDЕF.   Розглядаючи тінь  (при   різних   положеннях  площини    шестикутника   відносно площини стіни),   можна висловити декілька гіпотез про властивості паралельного  проектування. 

  Форму­ючи   ці   властивості,     припуст'имемо,  що проектування  здійснюється    паралельно   прямій    l, не паралельній прямим чи відрізкам, що проектуються.

Властивість 1. Проекція прямої є пряма.

Властивість 2.   Проекції   паралельних   прямих   паралельні.

Властивість 3. Відношення довжин проекцій двох паралельних відрізків дорівнює відношенню довжин відрізків, що проек­туються.

На цих доведеннях ми не спинятимемося.

Задачі на паралельне проектування у просторі.

1. Дано три різні точки. Скільки точок може утворитися на  площині проекцій при проектуванні даних точок? (одна, дві, три)

2. Якою фігурою є проекція проектуючої прямої? (точка)

3. Якою фігурою може бути проекція:

1) площини; (площиною або прямою)

2) півплощини; (півплощиною, променем або прямою)

3) кута, відмінного від розгорнутого (кутом,  променем або прямою)?

4. В якому випадку:

1) проекція точки збігається з цією точ­кою;  

2) проекція прямої збігається з цією прямою?

5. В якому випадку буде неправильним твердження: «Проек­ції паралельних прямих паралельні»? (Якщо ці прямі є проектуючими)

6. Відомо, що відрізок і його проекція мають рівні довжини. Як може бути розміщений даний відрізок відносно площини про­екцій?(паралельно)

7. 1) Які фігури можна дістати, проектуючи на площину об'єднання двох прямих, що перетинаються? (прямі, що перетинаються або пряму)

2) Які фігури можна дістати, проектуючи на площину об'єд­нання двох мимобіжних прямих? (прямі, що перетинаються або паралельні прямі і точку, яка не належить ій).

8. 1°) Якщо проекції двох прямих паралельні, то чи правильне
твердження, що паралельні  й прямі,  які проектуються?(ні).

2) Дано мимобіжні прямі а, b і площину проекцій a. Проведіть пряму l так, щоб при проектуванні паралельно l проекції прямих а і b були  паралельні.

9. З однієї точки виходять три промені, що не лежать в одній площині. Якою фігурою може бути проекція об'єднання цих про­менів? (об’єднання двох  або трьох різних променів, що мають спільний початок)

10. Відрізок АВ перетинає площину проекцій у точці М. Його проекцією є відрізок А₁В₁. Відомо: АВ= m, А₁М:МВ₁ = p:q. Знайдіть АМ і МВ. (mp(p + q)^-1; mq(p + q)^-1;

ЗОБРАЖЕННЯ   ФІГУР   У   СТЕРЕОМЕТРІЇ

У стереометрії зображенням фігури (оригіналу) називатимемо будь-яку фігуру, подібну паралельній проекції даної фігури на деяку площину. Для даної фігури форма її зображення залежить від положення оригіналу відносно площини проекцій, а також від вибору-прямої /, паралельно якій виконують проектування.

Задачу побудови зображення фігури вважають розв'язаною, якщо побудовано будь-яке зображення фігури, досить наочне і зручне для проведення на ньому додаткових ліній. Способи побу­дови зображень, якими ми будемо користуватися, грунтуються на властивостях паралельного проектування.

Д. Трикутник. Спостерігаю­чи тінь моделі трикутника,  природно припустити, що проекція цього трикутника може бути трикут­ником будь-якої форми. Правильне таке твердження: довільний трикут­ник, який лежить у площині проек­цій, можна вважати зображенням даного трикутника.

Зокрема, рівносторонній трикутник       можна зображати у вигляді будь-якого

різностороннього трикутника. Приходимо до висновку: при пара­лельному проектуванні величина кута і відношення довжин не-паралельних відрізків,  взагалі кажучи, не зберігаються.

Властивість  3 паралельної проекції дає можливість, зокрема, Зробити висновок, що медіана трикутника зображається медіаною зображення цього трикутника .

2.      Паралелограм. Оскільки паралельність прямих при
паралельному проектуванні зберігається, то зображенням пара­лелограма (зокрема, прямокутника, ромба, квадрата) є паралелограм Довжини сторін і величини кутів цього паралело­грама (зображення) можна взяти довільно.

Для обгрунтування останнього твердження досить застосувати правило зображення трикутника (пункт 1) до трикутника, утворе­ного після проведення діагоналі паралелограма-оригіналу (мал. 44).

3.      Трапеція. Властивості паралельної проекції дають можливість зробити висновок, що трапеція А1В1С1О1 зобразиться у вигляді трапеції АВСО , в якої відношення основ дорівнює відношенню основ оригіналу.

Рівнобедрена трапеція має вісь симетрії. Користуючись цим, побудуємо зображення висоти [ОЕ] цієї трапеції: \ВN\~^NА\, \СМ\=\МО\, №)\\(ММ).

Задачі

 1°. Трикутник АВС є проекцією трикутника . У трикутнику АВСпроведено з вершини бісектрису, медіану і висоту. Чи будуть проекції цих відрізків бісектрисою, медіаною і висотою АВС?

2. Дано зображення рівнобедреного трикутника у вигляді гдабізвостороннього трикутника. На цьому зображенні побудуйте: 1)зображення бісектриси кута при вершині, 2) зображення перпендикуляра до основи, проведеного через середину бічної сторони. 

3. Дано зображення трикутника і двох його висот. Побудуйте зображення  центра круга,  описаного навколо трикутника-оригінала

4. Чи може: 1) зображенням заданого чотирикутника бути довільний чотирикутник; 2) зображенням трапеції бути паралелограма; 3) зображенням ромба — квадрат?

5. 1) Які з властивостей ромба збережуться і в зображенні ромба? Які можуть не зберегтися? 2) Які властивості прямо­кутника збереже його проекція?

6.Трапеція АВСН є проекцією трапеції  на площину, що проходить через (АВ). Чи рівні довжини середніх ліній цих трапецій, якщо: 1) (АВ) \\ (СР); 

7.  На зображенні правильного шестикутника побудуйте зображення: 1) апофеми шестикутника; 2) бісектриси одного з його зовнішніх кутів; 3) перпендикуляра, проведеного через центр до однієї з менших діагоналей.

8.  Побудуйте на зображенні ромба зображення його висоти, якщо кут ромба дорівнює 45°.

9. Усі ребра тетраедра АВСВ мають рівні довжини, К — середина ребра ВВ. 

1) Побудуйте дві прямі КМ і Кії, які перпен­дикулярні відповідно до (АН) і (ОС) і перетинають їх у точках М і N. 

2) Побудуйте точку перетину площини СМН з прямою, яка сполучає вершину V і точку перетину медіан протилежної грані. 

3) Знайдіть площу трикутника КМИ, взявши довжину кожного ребра тетраедра такою, що дорівнює а.