Довжина вектора. Кут між векторами
Заголовок статті дає багато інформації про матеріал, який буде викладено далі. Він досить простий для засвоєння, однак важливий та потрібний в подальшому. На його основі будуть формулюватися всі наступні поняття розв'язуватися різні задачі на площині та здійснюватися обчислення.
Координати вектора 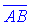 дорівнюють різниці відповідних координат кінця та початку вектора. Якщо
дорівнюють різниці відповідних координат кінця та початку вектора. Якщо 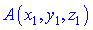 і
і 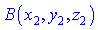 - відповідно початок та кінець вектора, то
- відповідно початок та кінець вектора, то
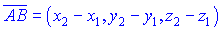
Довжиною або нормою вектора 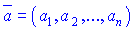 (позначають
(позначають  ) називають невід'ємне значення квадратного кореня з суми квадратів координат вектора, тобто
) називають невід'ємне значення квадратного кореня з суми квадратів координат вектора, тобто
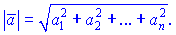
Для прикладу, якщо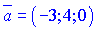 , то
, то
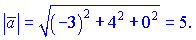 .
.
Для прикладу, якщо
Кутом між ненульовими векторами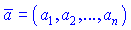 і
і 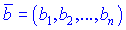 називається значення кута
називається значення кута 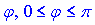 , яке визначається з рівності
, яке визначається з рівності
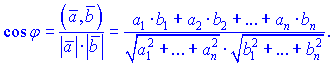
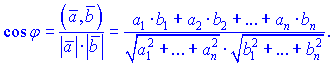
Приклад 1. Знайти довжину векторів 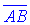 та
та  , якщо їх початки та кінці задані вершинами
, якщо їх початки та кінці задані вершинами
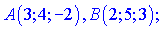
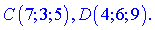
Розв'язок. Знайдемо вектори 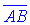 та
та 
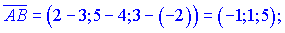
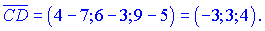
Обчислимо довжину векторів
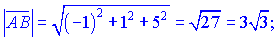
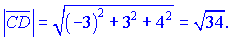
Знайдемо скалярний добуток векторів
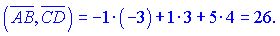
Знайдені значення підставляємо в формулу для обчислення кута між векторами
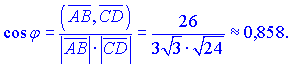
Звідси, остаточно знаходимо значення кута
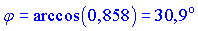
Вивчіть формулу довжини вектора, вона скоро Вам буде потрібно при вивченні наступних тем на вектори
Обчислимо довжину векторів
Знайдемо скалярний добуток векторів
Знайдені значення підставляємо в формулу для обчислення кута між векторами
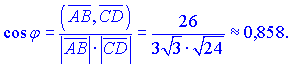
Звідси, остаточно знаходимо значення кута
Вивчіть формулу довжини вектора, вона скоро Вам буде потрібно при вивченні наступних тем на вектори
Немає коментарів:
Дописати коментар