Площа трикутника. Формули

Формул для обчислення площі трикутника в літературі можна знайти більше 10. Більшість з них можна застосувати в задачах з відомими сторонами та кутами трикутниками. Однак є ряд складних прикладів, в яких задано лише одна сторона і кути трикутника, або радіус описаного чи вписаного кола та ще одна характеристика. В таких випадках просту формулу застосувати не вдасться.
Задачі на трикутники вивчають в 7, 8 класі з вивчення простих властивостей, обчислення площі і периметра. В 9, 10 класі учні не тільки знають чим відрізняється прямокутний трикутник від рівнобедреного чи рівностороннього, а й з успіхом використовують теорему косинусів для знаходження сторін, формулу Герона, вміють розв'язати задачі про коло вписане або описане навколо трикутника. Але до всього потрібно приходити поступово не перевантажуючи пам'ять та можливості учнів. Тоді накопичені знання можна з успіхом застосувати до обчислення задач на трикутники будь-якої складності.
Наведені нижче формули дозволять розв'язати 95 відсотків задач в яких потрібно знайти площу трикутника. Перейдемо до розгляду поширених формул площі.
Розглянемо трикутник зображений на рисунку нижче

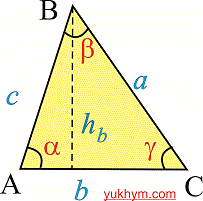
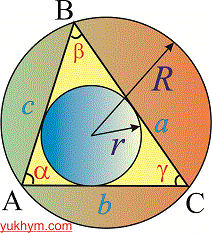
На рисунку і далі у формулах введені класичні позначення усіх його характеристик
a,b,c – сторонни трикутника,
R– радіус описаного кола,
r – радіус вписаного кола,
h[b],h[a],h[c] висоти, проведені відповідно до сторін a,b,c.
alpha, beta,hamma – кути при вершинах.

Основні формули площі трикутника

1. Площа трикутника рівна половині добутку сторони трикутника на висоту, опущену до цієї сторони. На мові формул це визначення можна записати так

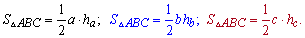
Таким чином, якщо відомо сторону та висоту, опущену до неї, то площу знайде кожен школяр.
До речі з цієї формули можна вивести одну корисну залежність між висотами

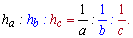
2. Якщо врахувати, що висота трикутника через сусідню сторону виражається залежністю

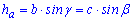
то з першої формули площі випливають однотипні другі

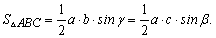
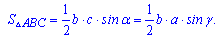
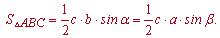
Уважно погляньте на формули – їх легко запам'ятати, оскільки в добутку фігурує дві сторони і кут між ними. Якщо правильно позначити сторонни і кути трикутника, то отримаємо дві сторонни a,b і кут пов'язаний з третьою С (hamma).

3. Для кутів трикутника справедливе співвідношення

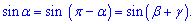
Залежність дозволяє застосовувати в обчисленнях наступну формулу площі трикутника

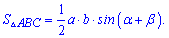
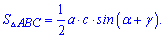
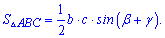
Приклади на дану залежність зустрічаються вкрай рідко, але пам'ятати, що є така формула Ви повинні.

4. Якщо відома сторона і два прилеглі кути, то площа знаходиться за формулою

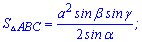
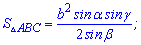
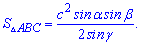
5. Формула площі трикутника через сторону і котангенси прилеглих кутів

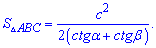
Перестановкою індексів можете отримати для інших сторін.

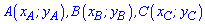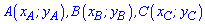6. Наведена нижче формула площі використовується в задачах коли вершини трикутника задані на площині координатами . В цьому випадку площа трикутника рівна половині визначника, взятого за модулем.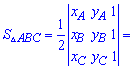

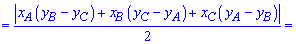
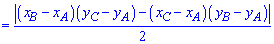
7. Формулу Герона застосовують в прикладах з відомими сторонами трикутника. Спочатку знаходять півпериметр трикутника

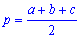
а далі визначають площу за формулою

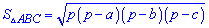
або

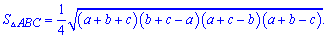
Її досить часто використовують в коді програм калькуляторів.

8. Якщо відомі всі висоти трикутника то площу визначають за формулою

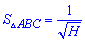
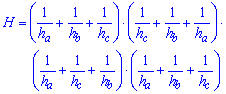
Вона складна для обчислення на калькуляторі, проте в пакетах MathCad, Mathematica, Maple площа знаходиться на «раз два».

9. Наступні формули вклячають відомі радіуси вписанного та описанного кіл (див. роисунок).

Зокрема, якщо відомо радіус і сторонни трикутника, чи його периметр то площа обчислюється згідно формули

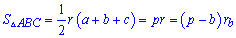
10. У прикладах де задано сторони і радіус (діаметр) описаного кола площу знаходять за формулою

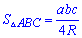
11. Наступна формула визначає площу трикутника через сторону і кути трикутника.

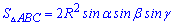
Ну і наостанок – часткові випадки:
Площа прямокутного трикутника з катетами a і b рівна половині їх добутку

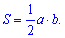
Формула площі рівностороннього (правильного) трикутника

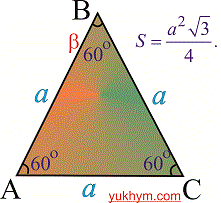
рівна одній четвертій добутку квадрату сторони на корінь з трійки.

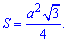
Приклад. Сторони трикутника рівні 3, 5, 6 см. Знайти площу трикутника.

Розв'язок: Застосуємо формулу Герона, для цього спочатку знайдемо півпериметр

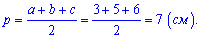
Підставляємо в формулу площі

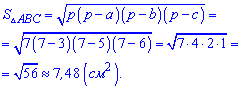
Відповідь: Площа трикутника рівна 7.48 сантиметрів квадратних.

Завантажити усі наведені формули площі трикутника Ви можете за наступним посиланням. Роздруковуйте їх та використовуйте в навчанні.