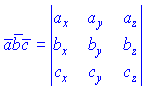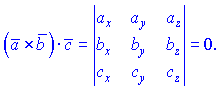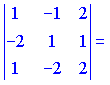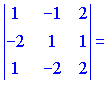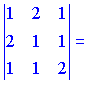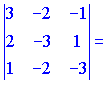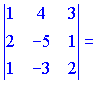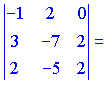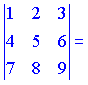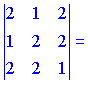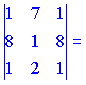Тетраедр в просторі (трикутна піраміда)
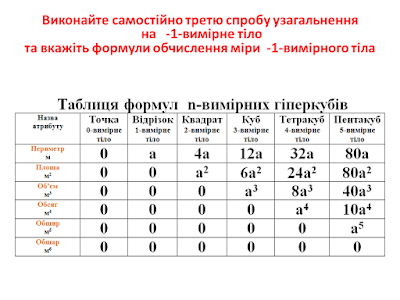
Перша спроба узагальнення на -1 вимірне тіло в геометрії Евкліда. Далі подана таблиця багатовимірних атрибутів в багатовимірних гіпертетраедрах. Поняття фігури ВЕРША, що має -1 вимір, виникає
при побудові систематизації у вигляді наступної таблиці:
В попередній статті ми обчислювали площу, рівняння висоти, медіани і бісектриси, якщо задано трикутник на площині 3 точками. З цієї статті Ви навчитеся обчислвати характеристики тривимірного тіла - тетраедра (трикутної піраміди). Крім розглянутих вище параметрів, тут потрібно знайти рівняння грані, довжину висоти, всеможливі кути, площу грані (трикутника), ну і на закуску об'єм піраміди. Розрахунків буде багато, тож не гайте часу і починайте вивчати інструкцію з обчислень.
Я і у випадку трикутника на площині, для трикутної піраміди ми теж написали відповідний код в математичному калькуяторі, але про це піде мова вкінці уроку.
Приклад 1. Тетраедр в просторі задано вершинами
A1(2;3;1), A2(4;2;1), A3(2;1;0), A4(5;2;10).
Потрібно знайти:
1) рівняння грані A1A2A3;
2) рівняння висоти піраміди, яка проходить через вершину A4 ;
3) довжину цієї висоти;
4) кут між ребром A1A4 і гранню A1A2A3 в градусах;
5) площу грані A1A2A3;
6) oб'єм піраміди.
Я і у випадку трикутника на площині, для трикутної піраміди ми теж написали відповідний код в математичному калькуяторі, але про це піде мова вкінці уроку.
Приклад 1. Тетраедр в просторі задано вершинами
A1(2;3;1), A2(4;2;1), A3(2;1;0), A4(5;2;10).
Потрібно знайти:
1) рівняння грані A1A2A3;
2) рівняння висоти піраміди, яка проходить через вершину A4 ;
3) довжину цієї висоти;
4) кут між ребром A1A4 і гранню A1A2A3 в градусах;
5) площу грані A1A2A3;
6) oб'єм піраміди.
Розв'язок.Виконуємо обчислення всіх величин в такому порядку.
1) Рівняння грані A1A2A3
Запишемо рівняння площини у вигляді
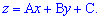 .
.
Оскільки всі три точки належать цій площині, то, підставляючи їх по черзі отримаємо систему рівнянь
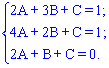
В результаті обчислень отримаємо значення
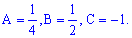 .
.
Підставляючи в початкове рівняння матимемо
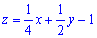 , або
, або 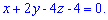 .
.
1) Рівняння грані A1A2A3
Запишемо рівняння площини у вигляді
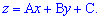 .
.Оскільки всі три точки належать цій площині, то, підставляючи їх по черзі отримаємо систему рівнянь
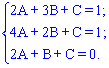
В результаті обчислень отримаємо значення
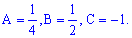 .
.Підставляючи в початкове рівняння матимемо
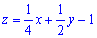 , або
, або 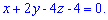 .
.
2) Рівняння висоти піраміди, яка проходить через вершину A4
Запишемо рівняння висоти піраміди, яка проходить через вершину A4
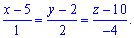 .
.
Запишемо рівняння висоти піраміди, яка проходить через вершину A4
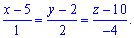 .
.
3) Висота, проведена з вершини A4
Знайдемо висоту, для цього знайдемо 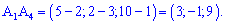
Висоту знайдемо враховуючи рівняння грані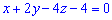 , за формулою
, за формулою
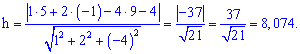
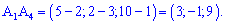
Висоту знайдемо враховуючи рівняння грані
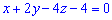 , за формулою
, за формулою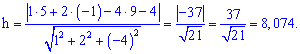
4) Кут между ребром A 1 A 4 и Гран A 1 A 2 A 3 в градусах
Знайдемо кут між ребром 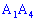 і гранню
і гранню 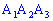 (
(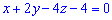 ) в градусах. Запишемо рівняння прямої, що проходить через точки
) в градусах. Запишемо рівняння прямої, що проходить через точки 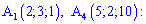
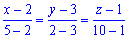 , або
, або 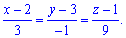
Знайдемо синус кута за формулою
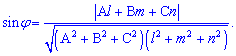
Підставимо значення
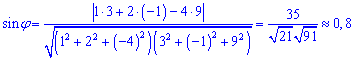
Знайдемо значення кута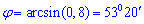
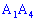 і гранню
і гранню 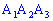 (
(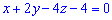 ) в градусах. Запишемо рівняння прямої, що проходить через точки
) в градусах. Запишемо рівняння прямої, що проходить через точки 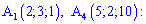
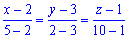 , або
, або 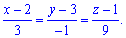
Знайдемо синус кута за формулою
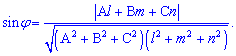
Підставимо значення
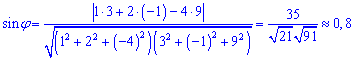
Знайдемо значення кута
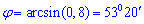
5) Площа грані A1A2A3
Площу грані 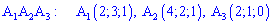 знайдемо за формулою модуля векторного добутку
знайдемо за формулою модуля векторного добутку
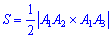
Обчислюємо вектори на яких побудована грань
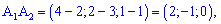
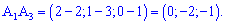
Знаходимо площу грані за формулою
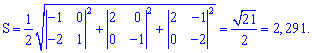
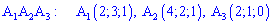 знайдемо за формулою модуля векторного добутку
знайдемо за формулою модуля векторного добутку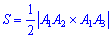
Обчислюємо вектори на яких побудована грань
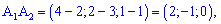
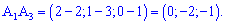
Знаходимо площу грані за формулою
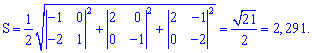
6) Об'єм піраміди
Знайдемо oб'єм піраміди за формулою мішаного добутку
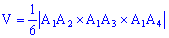 , де
, де
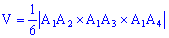 , де
, де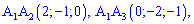
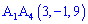
Складаємо визначник третього порядку та обчислюємо його
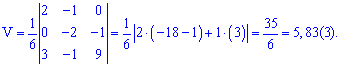
На цьому всі розрахунки.